|
|
|
Was ist eine Evolvente ?
|
|
|
|
Man stelle eine Rolle Bindfaden fest auf ein Blatt Papier, befestige am losen Fadenende einen Stift und wickle den Faden - straff gespannt - von der Fadenrolle ab. Die Linie, die der Stift auf dem Papier zeichnet, ist die (Kreis-)Evolvente der Fadenrolle.
|
|
|
|
Kann man das auch mathematisch präziser ausdrücken ?
|
|
|
|
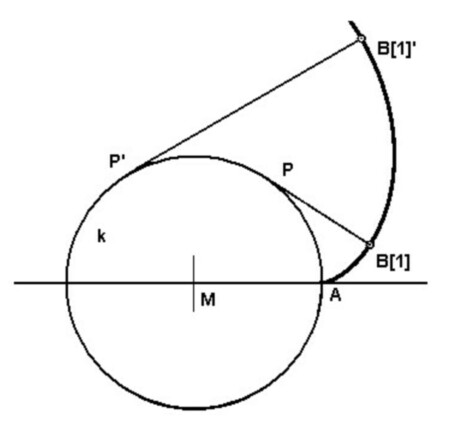
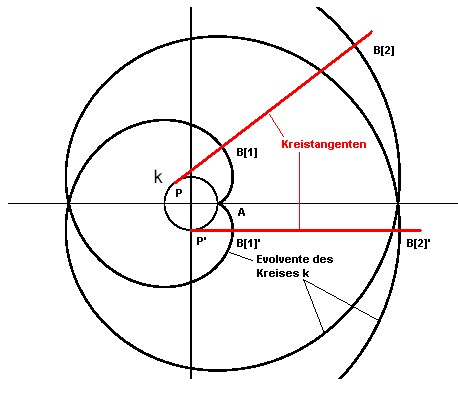
Gegeben sei ein beliebiger Punkt A auf dem Kreis k mit dem Mittelpunkt M. Dann lassen sich auf jeder Tangente an den Kreis k mit dem Berührungspunkt P Punkte B[n] (n = 1,2,...) so finden, daß die Summe aus der Länge des Kreisbogens AP und der Strecke PB[n] (bei differenzierbarem Übergang in P) gleich dem n-fachen des Umfanges des Kreises k ist. Der geometrische Ort der Punkte B[n] aller Kreistangenten an k heißt (Kreis-)Evolvente des Kreises k bezüglich des Punktes A.
|
|
|
|
|
erstes Teilstück einer Kreisevolvente
|
|
|
|
|
Kreisevolvente
|
|
|
|
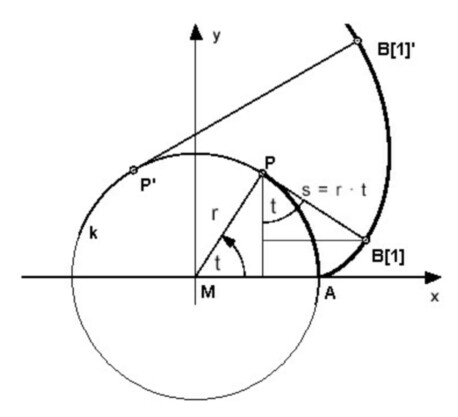
Die Parameterdarstellung der Punkte B der Kreisevolvente in Abhängigkeit vom Winkel AMP ( = t) lautet für den Einheitskreis (Mittelpunkt im Nullpunkt, Radius = r = 1, A = (1,0)):
|
|
|
|
B(x,y) = B(t) = B(cos(t)+t*sin(t),sin(t)-t*cos(t))
|
|
|
|
|
Herleitung der Parameterdarstellung
|
|
|
|
Hat das alles irgendeinen praktischen Sinn ?
|
|
|
|
Die wichtigste Anwendung findet die Evolvente in der technischen Mechanik: In Zahnradgetrieben beschreibt die Evolvente die Abrollkurve der Zahnflanken aufeinander, mit anderen Worten: Die Flanken eines Zahnrad-Zahnes haben die Form von Evolventen.
Auch im Sport spielt die Evolvente eine fast schon alltägliche Rolle: In jedem klassischen Leichtathletik-Stadion werden alle Läufe mit einer Länge über 800 Meter von einer Startlinie gestartet, die jedem Läufer - also auch denjenigen Läufern, die auf der Außenbahn antreten - die gleiche Entfernung zur Innenbahn garantiert.
|
|
|
 |
|
|